Перевод единиц измерения Крутящего момента. Единицы момента силы, единицы вращательного момента, единицы вертящего момента, единицы вращающего момента. Таблица
Содержание:
- 1 Что такое крутящий момент
- 2 Таблица перевода единиц измерения величин крутящего момента. Единицы момента силы, единицы вращательного момента, единицы вертящего момента, единицы вращающего момента.
- 3 Что такое лошадиные силы
- 4 Определение крутящих моментов и построение эпюры
- 5 Мощность двигателя
- 6 Соотношение крутящего момента к мощности
- 7 Расчет — момент
- 8 Расчет вала
- 9 1 Кинематический анализ механизма
- 10 Так что же важнее и лучше
- 11 Общие сведения
- 12 Специальные случаи
Что такое крутящий момент
У многих автомобилистов нет адекватного представления о том, что это за «зверь». О нем, впрочем, как и о мощности, бытует расхожее мнение: чем больше, тем лучше. По сути, это тесно связанные характеристики. Мощность в ваттах не что иное, как крутящий момент в ньютон-метрах, умноженный на число оборотов и на 0,1047. Другими словами, мощность демонстрирует количество работы, выполняемой двигателем за определенный промежуток времени, а крутящий момент отражает способность силового агрегата эту работу совершить. Если, скажем, автомобиль завяз в глинистом грунте и обездвижился, то производимая им мощность будет равняться нулю. Ведь работа не совершается. А вот момент, хотя его и не хватает для движения, присутствует. Крутящий момент без мощности существовать может, а мощность без момента — нет.

Главным достижением работающего мотора при превращении тепловой энергии в механическую является момент, или тяга. Высокие моментные значения характерны для дизельных двигателей, конструктивная особенность которых – большой (больше диаметра цилиндра) ход поршня. Большой крутящий момент у дизеля нивелируется относительно низким допустимым числом оборотов, которые ограничивают для увеличения ресурса. Высокооборотистым бензиновым моторам свойствен «крен» в сторону мощности, ведь их детали отличаются меньшим весом. И степень сжатия тоже ниже. Правда, современные силовые агрегаты – и дизельные, и бензиновые – совершенствуясь, становятся ближе и конструктивно, и по показателям. Но пока банальное правило рычага сохраняется: выигрывая в силе, проигрываешь в скорости. И, соответственно, в расстоянии.

Лучшие черты двигателя определяются совокупностью оптимальных значений мощности и тяги. Чем раньше наступает максимум крутящего момента и чем позже пик мощности, тем шире диапазон возможностей силового агрегата. Близкие к оптимальным характеристики имеют электрические двигатели. Они располагают тягой, близкой к максимальной, практически с начала движения. В то же время значение мощности прогрессивно возрастает. Существенным фактором в вопросах определения мощности и крутящего момента являются обороты двигателя. Чем они выше, тем большую мощность можно снять.

В этом контексте уместно упомянуть о гоночных моторах. Из-за относительно скромных объемов они не блещут умопомрачительным крутящим моментом. Однако способны раскручиваться до 15–20 тыс. оборотов в минуту (мин-1), что позволяет им выдавать супермощность. Так, если рядовой силовой агрегат при 4000 об/мин генерирует 250 Н∙м и порядка 140 л. с., то при 18 000 мин-1 он мог бы выдать в районе 640 л. с.
К сожалению, повышать частоту вращения довольно сложно. Мешают силы инерции, нагрузки, трение. Скажем, если раскрутить мотор от 6000 до 12 000 мин-1, то силы инерции возрастут вчетверо, что потенциально грозит опасностью перекрутить мотор. Повысить величину крутящего момента можно с помощью турбонаддува, но в этом случае негативную роль начинают играть тепловые нагрузки.
Принцип максимальной отдачи мощности красноречиво иллюстрируют моторы болидов «Формулы-1», имеющие весьма скромный объем (1,6 литра) и относительно невысокий показатель тяги. Но за счет наддува и способности раскручиваться до высоких оборотов выдают порядка 600 л. с. Плюс к тому, конструкция у «Ф1» – гибридная, и электродвигатель, дополняющий основной мотор, при необходимости добавляет еще 160 «лошадей».

Важной характеристикой, отражающей возможности мотора, является диапазон оборотов, при котором доступна максимальная тяга. Но еще важнее эластичность двигателя, то есть способность набирать обороты под нагрузкой
Другими словами, это соотношение между числами оборотов для максимальной мощности и оборотов для максимального крутящего момента. Оно определяет возможность снижения и увеличения скорости за счет работы педалью газа без переключения передач. Или возможность езды на высоких передачах с малой скоростью. Эластичность, к примеру, выражается способностью автомобиля разгоняться на пятой передаче с 80 до 120 км/ч на пятой. Чем меньше времени займет этот разгон, тем эластичнее двигатель. Из двух двигателей одинакового объема и мощности предпочтителен тот, у которого выше эластичность. При прочих равных условиях такой мотор будет меньше изнашиваться, работать с меньшим шумом и меньше расходовать топливо, а также облегчит работу трансмиссии.
А если все-таки задаться вопросом о том, что важнее – крутящий момент или мощность, деля мир на черное и белое, ответ будет предельно прост: так как это зависимые величины, важно и то и другое
Таблица перевода единиц измерения величин крутящего момента. Единицы момента силы, единицы вращательного момента, единицы вертящего момента, единицы вращающего момента.
| Перевести из: | Перевести в: | ||||||||||||||||
| Н*м | Н*см | Н*мм | кН*м | Дин*м | Дин*см | Дин*мм | кгс*м | кгс*см | кгс*мм | гс*м | гс*см | гс*мм | (Унция силы)*фут | (Унция силы)*дюйм | (Фунт силы)*фут | (Фунт силы)*дюйм | |
| Н*м (единица СИ) это: | 1 | 102 | 103 | 10-3 | 105 | 107 | 108 | 0.1019 | 10.1971 | 101.9716 | 101.9716 | 10197.1621 | 101971.6212 | 11.8009 | 141.6119 | 7.375*10-1 | 8.8507 |
| Н*см это: | 10-2 | 1 | 10 | 10-5 | 103 | 105 | 106 | 1.0197*10-3 | 0.1019 | 1.0197 | 1.0197 | 101.9716 | 1019.7162 | 1.180*10-1 | 1.416 | 7.3756*10-3 | 8.8507*10-2 |
| Н*мм это: | 10-3 | 10-1 | 1 | 10-6 | 102 | 104 | 105 | 1.0197*10-4 | 1.0197*10-2 | 1.0197*10-1 | 1.0197*10-1 | 10.1971 | 101.9716 | 1.18*10-2 | 1.4161*10-1 | 7.3756*10-4 | 8.85*10-3 |
| кН*м это: | 103 | 105 | 106 | 1 | 108 | 1010 | 1011 | 101.9716 | 10197.1621 | 101971.6212 | 101971.6212 | 10197162.1297 | 101971621.2977 | 11800.994 | 141611.9289 | 737.5621 | 8850.7454 |
| Дин*м это: | 10-5 | 10-3 | 10-2 | 10-8 | 1 | 102 | 103 | 1.02*106 | 1.0197*10-4 | 1.0197*10-3 | 1.0197*10-3 | 1.0197*10-1 | 1.0197 | 1.1801*10-4 | 1.4161*10-3 | 7.376*10-6 | 8.8507*10-5 |
| Дин*см это: | 10-7 | 10-5 | 10-4 | 10-10 | 10-2 | 1 | 10 | 10-8 | 1.02*10-6 | 1.0197*10-5 | 1.0197*10-5 | 1.0197*10-3 |
1.0197*10-2 |
1.18*10-6 | 1.4161*10-5 | 7.4*10-8 | 8.85*10-7 |
| Дин*мм это: | 10-8 | 10-6 | 10-5 | 10-11 | 10-3 | 10-1 | 1 | 10-9 | 1.02*10-7 | 1.02*10-6 | 1.02*10-6 | 1.0197*10-4 | 1.0197*10-3 | 1.18*10-7 |
1.416*10-6 |
7*10-9 | 8.9*10-8 |
| кгс*м это: | 9.8066 | 980.665 | 9806.65 | 9.8066*10-3 | 980665 | 9806657.2*102 | 980665*103 | 1 | 102 | 103 | 103 | 105 | 106 | 115.7282 | 1388.7387 | 7.233013576 | 86.7961 |
| кгс*см это: | 9.8*10-2 | 9.8066 | 98.0665 | 9.8066*10-5 | 9806.65 | 980665 | 9806650 | 10-2 | 1 | 10 | 10 | 103 | 104 | 1.1572 | 13.887 | 7.233*10-2 | 8.679*10-1 |
| кгс*мм это: | 9.8*10-3 | 9.8*10-1 | 9.8066 | 9.807*106 | 980.665 | 98066.5 | 980665 | 10-3 | 10-1 | 1 | 1 | 102 | 103 | 1.157*10-1 | 1.3887 | 7.233*10-3 | 8.679*10-2 |
| гс*м это: | 9.8*10-3 | 9.8*10-1 | 9.8066 | 0.000009807 | 980.665 | 98066.5 | 980665 | 10-3 | 10-1 | 1 | 1 | 102 | 103 | 1.157*10-1 | 1.3887 | 7.233*10-3 | 8.679*10-2 |
| гс*см это: | 9.8*10-5 | 9.8*10-3 | 9.8*10-2 | 9.8*10-7 | 9.8066 | 980.665 | 9806.65 | 10-5 | 10-3 | 10-2 | 10-2 | 1 | 10 | 1.15*10-3 | 1.3887*10-2 | 7.233*10-5 | 8.679*10-4 |
| гс*мм это: | 9.8*10-6 | 9.8*10-4 | 9.8*10-3 | 10-8 | 9.8*10-1 | 98.0665 | 980.665 | 10-6 | 10-4 | 10-3 | 10-3 | 10-1 | 1 | 1.15*10-4 | 1.3887*10-3 | 7.233*10-6 | 8.679*10-5 |
| (Унция силы)*фут это: | 8.47*10-2 | 8.4738 | 84.7386 | 8.474*10-5 | 8473.8624 | 847386.24 | 8473862.4 | 8.641*10-3 | 8.64*10-1 | 8.6409 | 8.6409 | 864.0934 | 8640.9348 | 1 | 12 | 6.249*10-2 | 7.499*10-1 |
| (Унция силы)*дюйм это: | 7*10-3 | 7.061*10-1 | 7.0615 | 7.062*10-6 | 706.1552 | 70615.52 | 706155.2 | 7.2*10-4 | 7.2*10-2 | 7.2*10-1 | 7.2*10-1 | 72.0077 | 720.077906319 | 8.3*10-2 | 1 | 5.2083*10-3 | 6.2499*10-2 |
| (Фунт силы)*фут это: | 1.3558 | 135.5818 | 1355.818 | 1.35*10-3 | 135581.8 | 13558180 | 135581800 | 1.382*10-1 | 13.8254 | 138.2549 | 138.2549 | 13825.4959 | 138254.9596 | 16.000000189 | 192.000002266 | 1 | 12 |
| (Фунт силы)*дюйм это: | 1.129*10-1 | 11.2984 | 112.9848 | 1.129*10-4 | 11298.48 | 1129848.3 | 11298483.3 | 1.152*10-2 | 1.1521 | 11.5212 | 11.5212 | 1152.1246 | 11521.2466 | 1.333 | 16.000000189 | 8.33*10-2 | 1 |
Что такое лошадиные силы
Наблюдательный читатель, скорей всего, отметит подозрительным тот факт, что до сих пор не прозвучало, всеми так любимое «лошадиные силы». Суть в том, что «скакуны» — это лишь дань моде тех времен, когда механизмам приходилось доказывать свое преимущество над живой рабочей силой. Поэтому превосходство (способность выполнить определенное количество работы) удобно было выражать в пересчете на потенциал одной лошади. Фактически 1 л.с – это усилие, которого достаточно для поднятия груза массою 75 кг на 1 м за 1 с.
Для того чтобы получить «лошадиные силы» достаточно умножить значение мощности в киловаттах на коэффициент 1,36.
Покупатели не потеряют ровным счетом ничего, если производители откажутся использовать «л.с» в качестве показателя мощностных характеристики автомобилей. Обозначить крутящий момент и мощность в кВт вполне достаточно. Но традиция настолько глубоко запечатлелась в сознании, что тратить усилия на ее разрушения попросту нецелесообразно.
Итоги
- Мощность мотора зависит от крутящего момента;
- «л.с» рассчитаны на достижение максимальной скорости. Автомобиль с большим количеством «скакунов» под капотом сможет развить внушительную скорость, но это займет очень много времени;
- от тягового усилия зависит насколько быстро двигатель сможет развить свою максимальную мощность;
- большое количество «ньютон-метров» позволяет более выгодно использовать потенциал двигателя. Такие моторы легче переносят нагрузки;
- чем шире «полка» момента, тем эластичней двигатель и приятней в управлении автомобиль;
- ввиду особенностей дизельных ДВС (большая степень сжатия, медленное горение смеси), а также применения современных систем дополнительного нагнетания воздуха, дизельные двигатели имеют больший крутящий момент с самих низких оборотов.
Выражаясь простым языком, «ньютон-метры» – это сила вашего автомобиля, а киловатты – выносливость.
Определение крутящих моментов и построение эпюры
2010-03-12
Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент Mк.
Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.
Крутящий момент для сечения можно выразить так: $$M _к(x) = \sum M _{кi} + \sum \int m _i(x)\cdot dx$$

Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид:
$$M _к(x) = \sum M _{кi} + \sum m _i(x)\cdot (x- L_{mн}) — \sum m _i(x)\cdot (x- L_{mк})$$
где Lmн и Lmк – расстояние от начала координат до начала и до конца распределенного момента соответственно.
Дифференциальная зависимость внутренних усилий от распределенной нагрузки m:
dMк = m·dx
Общий порядок расчета и построения эпюры.
- Намечаем характерные сечения стержня.
- Определяем крутящий момент в каждом характерном сечении.
- По найденным значениям моментов строим эпюру.
Построение эпюр крутящих моментов (пример)
Построить эпюру крутящих моментов для жестко защемленного стержня
 Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1=-30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).
Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1=-30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).
1. Число характерных сечений — 6
Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.
2. Проведем сечение 1. Определим крутящий момент в текущем сечении:
Mк1= Mкв2= 50 кНм
3. Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом Mк2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:
Mк2 = Mк1 = Mкв2 = 50 кНм
3. Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:
Mк3 = Mкв2 – m1*4 = 50 – 10*4 = 10 кНм
4. Аналогично для сечения 4:
Mк4 = Mк3 = 10 кНм
5. Также для сечения 5:
Mк5= Mк4-Mкв1= 10 – 30 = -20 кНм
6. Для сечения 6:
Mк6= Mк5 =-20 кНм
7. По полученным значения строим эпюру крутящих моментов (см. рис.).
Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) Mк6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.
Правила контроля правильности эпюр крутящих моментов
Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.
- Эпюры крутящих моментов всегда прямолинейные.
- На участке, где нет распределенных моментов, эпюра Mк – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
- Под точкой приложения сосредоточенного момента на эпюре Mк будет скачок на величину этого момента.
Дополнительно
Пример из пособия МИИТ Построение эпюры крутящих моментов (формат pdf).
1 В технике употребляется терминология «винт с правой резьбой» или «винт с левой резьбой». На винт с правой резьбой гайка навертывается при вращении по часовой стрелке (т.е прикладываем положительный момент Mк ), а свинчивание гайки происходит при вращении влево (т.е прикладываем отрицательный крутящий момент ).
Мощность двигателя
Измеряется в «Лошадиных Силах (л.с.)» или Киловаттах (Ваттах, «Вт»), как становится понятно — ей занимался Джеймс Ватт. Да, именно в Ваттах мы измеряем мощность лампочки накаливания у нас в «люстрах» и светильниках, но оказывается и мощность двигателя тоже. Я не буду вдаваться в подробности, как и что он открыл, просто характеристика идет именно от его фамилии. НО как же лошадиные силы? А все просто, Ватт «тренировался» на лошадях, а именно на переносимых грузах, одной лошадью в единицу времени и на определенное расстояние, так вот после определенных «терзаний» выяснилось — что одна лошадь (если ее заставить генерировать электрический ток, от динамомашины) способна выдавать 736 Ватт в секунду времени, либо 75 кгс м/с, что можно расшифровать так — 75 килограмм, на 1 метр высоты, за 1 секунду времени. Чтобы перевести «ватты» в «лошадиные силы», существует достаточно большой расчет, но если утрировать, то получается 1кВт=1000Вт=1,36л.с.

Не все производители указывают мощность двигателя в «л.с.», например некоторые немецкие производители указывают именно в Ваттах.
Думаю это понятно, больше к этому возвращаться не будем.
Мощность двигателя внутреннего сгорания (будь то это бензин или дизель), величина не постоянная! ЭТО НУЖНО ПОНИМАТЬ! Меня просто умиляет то, как многие реагируют на эту величину: — у меня 150 л.с., я тебя сделаю как «два пальца», а у оппонента 145 л.с. и по теории он должен проиграть, но не учитывается крутящий момент и расстояние, на котором будут соревноваться автомобили.
Мощность изменяется от оборотов двигателя! Ваша номинальная величина, будет указана при определенных МАКСИМАЛЬНЫХ оборотах, у современных авто, обычно от 5000 до 6500 оборотов. ТО есть простыми словами, 150л.с. – выдаются при 6000 оборотов (для примера). Соответственно при 3000 или при 1500 оборотов, мощность будет уменьшаться в разы.
ТО есть, для того чтобы получить весь «табун» силового агрегата, вам нужно активно «педалировать». Например — при обгонах или резких маневрах, вы должны держать почти вашу «полку» в 5000 – 6500 оборотов именно эти обороты вам помогут резко ускориться. Вот почему зачастую приходится понижать передачу, для того чтобы получить максимум мощности.
НО силовой агрегат не может мгновенно раскрутиться, ему на это нужно время, здесь то и приходит такое понятие как крутящий момент.
Соотношение крутящего момента к мощности
Для получения наглядного представления о взаимодействии двух величин рассмотрим основные характеристики мотора на графике. Он демонстрирует выдаваемую двигателем мощность и крутящий момент двигателя в зависимости от оборотов коленчатого вала.

График отчетливо демонстрирует тот факт, что тяговое усилие на колесах не прямо пропорционален количеству оборотов либо мощности. Двигатель достигает пика крутящего момента уже на 3 тыс. об/мин. Максимум мощности доступно на 5500 об/мин. В обоих случаях обороты продолжают расти, но отдача падает. Для обозначенного двигателя обороты от 2500 до 5 тыс. наиболее оптимальные.
Приведенный график является примером гражданской настройки современных бензиновых моторов. Преимущества очевидны:
- стабильный прирост мощности;
- достаточно широкая «полка» с плавным приростом и затуханием.
Настройка подобного типа позволяет добиться «эластичности» двигателя. Такая работа обеспечивается не только программно (настройка ЭБУ), но и применением различных вспомогательных технологий (изменяемые фазы газораспределения).
Разница мощностных характеристик во многом зависит от конструкции системы впуска и выпуска. К примеру, двигатели оснащенные турбонаддувом в точке выхода на «буст» получают значительную прибавку в динамике. Крутящий момент и количество лошадиных сил таких моделей значительно превышают своих атмосферных собратьев.
Расчет — момент
Расчет момента производится, исходя из того, что в месте контакта головки шпинделя с опорой создается площадка диаметром 1Ш ( фиг.
Расчет момента производится, исходя из того, что в месте контакта головки шпинделя с опорой создается площадка диаметром Аш ( фиг.
Расчет моментов и усилий уточняется по кинематической схеме СРП, разрабатываемой на этапе технического проектирования.
Расчет момента приведен без учета потерь на трение в направляющих фиксирующей детали и звездочки.
Расчет моментов и усилий в кинематической цепи ведется от ведомых звеньев к ведущему. Такая последовательность расчета связана с тем, что нагрузки концевых ведомых звеньев цепи обычно бывают известны или легко вычисляются.
Расчет момента приведен без учета потерь на трение в направляющих фиксирующей детали и звездочки.
Расчет моментов и усилий в кинематической цепи ведется от ведомых звеньев к ведущему. Такая последовательность расчета связана с тем, что нагрузки концевых ведомых звеньев цепи обычно бывают известны или легко вычисляются.
Расчет моментов упрощается, если воспользоваться аппаратом характеристических функций.
Расчет моментов и усилий в механизмах ведется от конечных ведомых звеньев к ведущему. Подсчитанные или известные моменты трения или силовые нагрузки концевых ведомых звеньев должны быть приведены к ведущему звену через все промежуточные передачи с учетом их собственных моментов.
Расчет моментов М и М аналогичен определению сопротивлений Т и Т для блоков ( см. стр.
Расчет моментов, изгибающих шатунную шейку, приведен в табл. 60, где значения К.
Расчет момента нагрузки относительно оси вращения устройства.
Расчет момента внешних сил в массовых расходомерах, закручивающих измеряемый поток, по средней струйке потока или средней скорости дает приближенное значение. Точный расчет следует производить по всему сечению каналов крыльчаток.
|
Свойства растворителей, используемых при определении моментов диполя. |
Расчет момента диполя молекулы путем определения величины положительных и отрицательных зарядов и центров их тяжестей является сложной задачей, решаемой лишь отчасти применением квантовой механики. Проведение квантовохимических расчетов даже для относительно небольших молекул ( до 10 атомов) с учетом всех электронов не всегда выполнимо из-за недостаточной мощности ЭВМ или большой затраты машинного времени. Расчеты же, проводимые для сопряженных систем в л-электронном прибл — жении, хотя и позволяют рассматривать большие молекулы, не могут быть признаны удовлетворительными вследствие низкой точности.
Расчет вала
Условие задачи:
К стальному валу, состоящему из 4-х участков длиной l1…l4 приложено четыре сосредоточенных момента М1…М4 (см. рис. 1 ).

Требуется:
Построить эпюру крутящих моментов Мкр, подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений τmax, построить эпюру углов закручивания φ вала и определить наибольший относительный угол закручивания вала.
Нагрузки, кН×м:
- М1 = -4,5;
- М2 = -2,6;
- М3 = -3,1;
- М4 = -2,0;
Длина участков, м:
- l1 = 0,9;
- l2 = 0,6;
- l3 = 0,9;
- l4 = 0,4;
Указания:
Вычертить схему вала в соответствии с исходными данными.
Знаки моментов в исходных данных означают: плюс – момент действует против часовой стрелки относительно оси Z, минус – по часовой стрелке (см. навстречу оси Z). В дальнейшем значения моментов принимать по абсолютной величине.
Участки нумеровать от опоры.
Допускаемое касательное напряжение для стали принимать равным 100 МПа.
Решение:
1. Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала.
Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.
- МIV = -М1 = -4,5 (кН×м);
- МIII = -М1 — М2 = -4,5 — 2,6 = -7,1 (кН×м);
- МII = -М1 — М2 – М3 = -4,5 – 2,6 – 3,1 = -10,2 (кН×м);
- МI = -М1 — М2 – М3 – М4 = -4,5 – 2,6 – 3,1 – 2,0 = -12,2 (кН×м).
2. Подберем сечение вала из расчета на прочность при кручении по полярному моменту сопротивления для участка, где величина крутящего момента максимальная (без учета знака):
WP≥ Мкр/ .
Так как для круглого сечения полярный момент равен: Wр = πD3/16, то можно записать:
D ≥ 3√(16Мкр/π) ≥ 3√(16×12,2×103/3,14×) = 0,0855 м или D ≥ 85,5 мм.(Здесь и далее знак «√» означает квадратный корень из выражения)
В соответствии со стандартным рядом, предусмотренным ГОСТ 12080-66, принимаем диаметр вала D = 90 мм.
3. Определим угол закручивания для каждого участка вала по формуле:
φ = Мкр×l/G×Iр,
где G – модуль упругости 2-го рода; для стали G = 8×1010 Па;Ip – полярный момент инерции (для круглого сечения Iр = πD4/32 ≈ 0,1D4, м4).
Произведение G×Iр = 8×1010×0,1×0,094 ≈ 524880 Н×м2 – жесткость сечения данного вала при кручении.
Расчитываем углы закручивания на каждом участке:
- φI = -12,2×103×0,9/524880 = -0,0209 рад;
- φII = -10,2×103×0,6/524880 = -0,0116 рад;
- φIII = -7,1×103×0,9/524880 = -0,0122 рад;
- φIV = -4,5×103×0,4/524880 = -0,0034 рад.
4. Определяем углы закручивания сечений вала, начиная от жесткой заделки (опоры):
- φ0-0 = 0 рад;
- φ1-1 = φI= -0,0209 рад;
- φ2-2 = φI + φII= -0,0209 — 0,0116 = -0,0325 рад;
- φ3-3 = φI + φII + φIII= -0,0209 — 0,0116 — 0,0122 = -0,0447 рад;
- φ4-4 = φI + φII + φIII + φIV = -0,0209 — 0,0116 — 0,0122 -0,0034 = -0,0481 рад.
5. Определяем максимальное касательное напряжение на каждом силовом участке по формуле:
τmax = Мкр/Wp = 16Мкр/πD3≈ 5Мкр/D3.
Тогда:
- τmaxIV = 5×-4,5×103/0,093 = -30864197 Па ≈ -30,086 МПа;
- τmaxIII = 5×-7,1×103/0,093 = -48696844 Па ≈ -48,700 МПа;
- τmaxII = 5×-10,2×103/0,093 = -69958847 Па ≈ -69,959 МПа;
- τmaxI = 5×-12,2×103/0,093 = -83676268 Па ≈ -83,676 МПа.
6. Наибольший относительный угол закручивания Θmax определим по формуле:
Θmax = МКРmax/G×Iр = -12,2×103/524880 = 0,0232 рад/м.
7. По результатам расчетов строим эпюры крутящих моментов Мкр, касательных напряжений τmax и углов закручивания φ (см. рис. 2).

***
Учебные дисциплины
- Инженерная графика
- МДК.01.01. «Устройство автомобилей»
- Общее устройство автомобиля
- Автомобильный двигатель
- Трансмиссия автомобиля
- Рулевое управление
- Тормозная система
- Подвеска
- Колеса
- Кузов
- Электрооборудование автомобиля
- Основы теории автомобиля
- Основы технической диагностики
- Основы гидравлики и теплотехники
- Метрология и стандартизация
- Сельскохозяйственные машины
- Основы агрономии
- Перевозка опасных грузов
- Материаловедение
- Менеджмент
- Техническая механика
- Советы дипломнику
Олимпиады и тесты
- «Инженерная графика»
- «Техническая механика»
- «Двигатель и его системы»
- «Шасси автомобиля»
- «Электрооборудование автомобиля»
1 Кинематический анализ механизма
Рассчитать привод подъёмно-качающегося стола, схема которого приведена на рис.1, нагрузочная диаграмма угловой скорости на рис.2

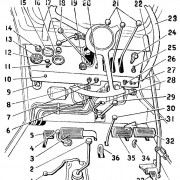
Рис. 1. Кинематическая схема подъёмно-качающегося стола:
| 1 — слиток; 2 — стол; 3 — штанга; 4 — трёхплечий рычаг; |
5 — контргруз; 6 -шатун; 7 — кривошип; 8 — редуктор. |

В таблице 1 приведены значения параметров для варианта 1.
Таблица 1
| 1 | Вес слитка, кН, Gсл | 30 |
| 2 | Вес стола, кН, Gст | 800 |
| 3 | Вес контргруза, кН, Gгр | 208 |
| 4 | Длина слитка, м, Lсл | 2,4 |
| 5 | Расстояние Оз А, м, Lа |
8,2 |
| 6 | Длина стола, м, Lст | 10 |
| 7 | Радиус кривошипа, м, rкр | 0,35 |
| 8 | Длина шатуна, м, Lш | 3,0 |
| 9 | Радиус 1 го рычага, м, rl | 0,65 |
| 10 | Радиус 2 го рычага, м, r2 | 0,7 |
| 11 | Радиус 3 го рычага, м, r3 | 1,7 |
| 12 | Угол наклона рычагов к горизонту, град, γ | 5 |
| 13 | Число циклов в час, 1/ч, Z | 170 |
| 14 | Время работы, с, toб | 8,4 |
| 15 | Угловая скорость двигателя, рад/с, ωдв | 75 |
По нагрузочной диаграмме угловой скорости (рис.2) определим:
значение угловой скорости ω
max
;
зависимость угловой скорости от угла поворота φ
кривошипа;
вычислим передаточное число редуктора.
Разобьем нагрузочную диаграмму на участки I, II, III.
Участок
I
Время изменяется в пределах
движение равноускоренное, угол поворота определим по формуле
где:
ε
I
– угловое ускорение рад/с.,
t
– время в с
.,
φ
– угол поворота.
ε
I
-находим из условия, что к моменту 0.1t, ω
I
= 0.7ω
max
,
Так как в начальный момент ω
= 0
поэтомуω = ε
t
,
следовательно
(2)
Уравнение вращательного движения на I участке примет вид
Угол поворота φ
на участке I к моменту 0.1to
б

Из выражения (3) выразим t
.
подставим в выражение (1) уравнение движения (5) и закон изменения угловой скорости (2), получаем

Отсюда:
(7)
Участок
II
Время изменяется в пределах
движение равноускоренное, угловое ускорение определим по формуле
Где:
∆ω
– изменение скорости за весь второй участок
1 ω
ma
x
— 0,7 ω
ma
x
= 0,3ω
ma
x
;
∆
t
– изменение времени за весь второй участок
0,7to
б
— 0,1to
б
= 0,6to
б
.
Уравнение вращательного движения на этом участке
φ
=
φо
+
ωо
(t-to
)+
ε
(t-to
)2
/
2
φо
– угол поворота в начале участка II(конец участка I),
to
– начальный момент времени для участка II,
ωо
– скорость вращения в начале участка II.
Подставляя все значения, получаем
φ =
0,035
ω
max
to
б
+0,7
ω
max
(
t
— 0,1
to
б
)+ 0,5
ω
max
(
t
— 0,1
to
б
)2
/2
to
б
(9)
Выражение (9)
при t
=0,1
to
б
(начало участка
II
)
даетзначение φ
= 0,035ω
max
to
б
при t
=0,7
to
б
(конец участка
II
)
дает значениеφ
= 0,545 ω
max
to
б
Закон изменения скорости на участке II примет вид
Подставим значение ω
=0,7
ω
max
и

Отсюда
t

Из этого выражения выразимω
II

Участок
III
Время изменяется в пределах
Так как движение равнозамедленное, отрицательное угловое ускорение определим по формуле
Где:
∆ω
– изменение скорости за весь третий участок ∆ω
=
ω
max
;
∆
t
– изменение времени за весь третий участок ∆
t
= 1 — 0,7
to
б
.= 0,3
to
б
Закон изменения скорости на участке III примет вид
Уравнение вращательного движения на этом участке
φ
=
φо
+
ωо
(t-to
)+
ε
III
(t-to
)2
/
2
φо
– угол поворота в начале участка III(конец участка II), φ =
0,545 ω
max
to
б
to
– начальный момент времени для участка III,to
= 0,7
to
б
ωо
– скорость вращения в начале участка III- ωо
= ω
max
.
Подставляя все значения, получаем
φ =
0,545 ω
max
to
б
+
ω
max
(
t
— 0,7
to
б
) —
ω
max
(
t
— 0,7
to
б
)2
/0,6
to
б
(17)
Выражение (17)
при t
= 0,7
to
б
(начало участка
III
)
даетзначение φ
= 0,545 ω
max
to
б
при t
=
to
б
(конец участка
III
)
дает значение
φ
= 0,545 ω
max
to
б
+ 0,3
ω
max
to
б
—
ω
max
(0,09
to
б
2
)/0,6
to
б
=0,695ω
max
to
б
Из выражения (16) выразим t
и подставим в выражение (17). Преобразовывая, получим.

Из этого выражения выразимω
III

Значение ωmax
определим из выражения (17) при t
=
to
б
(конец участка
III
)
φ
=0,695ω
max
to
б
.
Полный оборот φ =
2π
выходной вал редуктораделает заto
б
=8,4с
,
поэтомуω
max
= 2π/0,695
to
б
= 1,05рад/с
Так что же важнее и лучше
Здесь сложно сказать одно выходит из другого. С одной стороны момент, позволит развивать вам быстро максимальную мощность, в примере с дизелем, но он не сможет крутиться до таких оборотов как бензин, а значит его максимальная мощность в пике будет ниже. Тут знаете, кому что нужно, может быть вы водитель коммерческого транспорта, и вам не нужна максимальная скорость но важна тяга «с низов». Или наоборот, вы любите турбо моторы, которые крутятся до 8000 – 9000 оборотов и выстреливают с места.

Лично мне нравятся новые бензиновые агрегаты, такие как скажем у МАЗДЫ, мотор Skyactiv которые сейчас устанавливаются на многие модели. Здесь увеличили степень сжатия, немного приблизили мотор к дизелю, но он остался бензиновым с высокими оборотами. Здесь есть и мощность и крутящий момент, золотая середина! Думаю за такими моторами будущее (если не брать гибриды и электромобили).
И запомните: — крутящий момент толкает машину вперед, а вот мощность это то, что этот момент производит. Так что покупаем лошадиные силы, а ездим на моменте!
Сейчас видео версия статьи, смотрим.
А сейчас голосование, что вы считаете важнее – крутящий момент или мощность двигателя.
НА этом заканчиваю, читайте наш АВТОБЛОГ, подписывайтесь на канал в YOUTUBE.
Общие сведения
В момент силы можно понимать как «вращающая сила». В единицей измерения момента силы является (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как :
- M→=r→×F→,{\displaystyle {\vec {M}}=\left,}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — частицы (в предположении, что ось вращения проходит через начало координат).
Специальные случаи
Формула момента рычага

Момент, действующий на рычаг
Очень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=,ΣV={\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM={\displaystyle \Sigma M=0}.
Момент силы как функция от времени
Момент силы — по времени от ,
Видеоурок: вращающий момент
- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение и относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+M(ro→−rc→),vc→.{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+.}
Будем рассматривать вращающиеся движения в системе , так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — , измеряемое в в за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- Mc→=Icdω→dt+w→,Icw→.{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+.}