Абсолютная температура
Содержание:
Определение — абсолютная температура
Определения абсолютной температуры были выполнены при помощи нагревания в переменном магнитном поле.
Определения абсолютной температуры были выполнены в Лейдене, где использовался нагрев в переменном поле и гистерезисный нагрев, а также в Оксфорде, где применялись у-лучи.
Определения абсолютной температуры были выполнены в Лейдене при помощи нагревания в переменном магнитном поле п в Оксфорде, где использовались у-лучи. Эксперименты с церемонным полем были выполнены при температурах ниже максимума восприимчивости, поскольку выше него — / было слишком мало.
Определения абсолютной температуры были выполнены при помощи нагревания в неременном магнитном иоле.
Определения абсолютной температуры были выполнены Б Лейдене, где использовался нагрев в переменном поле и гисчерезнспын нагрев, а также л Оксфорде, где применялись у-лучп.
Определения абсолютной температуры были выполнены в Лейдене при помощи нагревания в переменном магнитном ноле п н Оксфорде, где использовались у-лучп. Эксперименты с переменным нолем были выполнены при температурах ниже максимума восприимчивости, поскольку выше него /; было слишком мало.
Из определения абсолютной температуры Т следует, что при температуре абсолютного нуля ( Т 0) тепловое движение молекул прекращается.
Для определения абсолютных температур вблизи нуля шкалы Кельвина выражение ( 33) можно записать в другой более удобной форме.
Для определения абсолютной температуры прежде всего необходим вторичный термометр, который должен быть програ-дуирован по абсолютной шкале температур. При более высоких температурах это не вызывает затруднений. Термометр может быть проградуирован отдельно и затем приведен в тепловой контакт с веществом, температура которого измеряется.
При идеализированном определении абсолютной температуры как меры движения газовых молекул абсолютный нуль определяется как такое состояние, в котором исчезает молекулярное движение. В настоящее время это представление признается неверным, независимо от того, конденсируется ли данный газ при низких температурах, переходя в твердое или жидкое состояние, или нет; однако в этой части курса такое упрощенное представление следует изложить как констатацию факта, не объясняя его подробнее, чем это сделано в Учебнике. Абсолютный нуль-это, по определению, такая температура, при которой любая система находится на самом низком энергетическом уровне, какой только возможен, но это состояние системы вовсе не соответствует полному отсутствию движения.
Из самого определения абсолютной температуры Т следует, что она всегда положительна. При температуре абсолютного нуля ( 7 0) тепловое движение молекул прекращается.
Из самого определения абсолютной температуры следует, что она отрицательной быть не может. За начало отсчета абсолютной температуры принят абсолютный нуль, теоретически определяемый.
Анализ возможностей определения абсолютных температур ниже 1 К был опубликован Джиоком в 1953 г. Автор отметил технические трудности, возникающие в описанном методе, при котором требуется сообщение тепла системе при температурах ниже 1 К, и описал метод, не требующий добавления тепла при этих температурах.
Магнитные методы определения абсолютной температуры в случае этой соли сопряжены с трудностями.
Зависимость ек от Т дает определение абсолютной температуры. Термодинамическая температура является физической величиной, пропорциональной средней кинетической энергии поступательного движения молекул идеального газа.
Взаимодействие атомов между собой
При
рассмотрении реальных
газов —
газов,
свойства которых зависят от взаимодействия
молекул, надо учитывать силы
межмолекулярного взаимодействия. Они
проявляются
на расстояниях 10-9
м и быстро убывают при увеличении
расстояния между молекулами. Такие
силы называются короткодействующими.
В XX
в., по мере развития представлений о
строении атома и квантовой механики,
было выяснено, что между молекулами
вещества одновременно действуют силы
притяжения и силы отталкивания. На
рис. 88, а
приведена
качественная зависимость сил
межмолекулярного взаимодействия от
расстояния r
между молекулами, где Fo
и Fп—
соответственно силы отталкивания и
притяжения, a
F—
их результирующая. Силы отталкивания
считаются положительными,
а
силы взаимного притяжения —
отрицательными.
На
расстоянии r
= rрезультирующая
сила F=0,
т. е. силы притяжения и отталкивания
уравновешивают друг друга. Таким
образом, расстояние rсоответствует
равновесному расстоянию между молекулами,
на котором бы они находились в отсутствие
теплового движения. При r
преобладают
силы отталкивания (F>0),
при r>r
— силы притяжения (F10-9
м межмолекулярные силы взаимодействия
практически отсутствуют (F0).
Элементарная
работа A
силы Fпри
увеличении расстояния между молекулами
на drсовершается
за счет уменьшения взаимной
потенциальной энергии молекул, т. е.
A=Fdr=-dП.
(60.1)
Из
анализа качественной зависимости
потенциальной энергии взаимодействия
молекул от расстояния между ними
(рис. 88, б)
следует,
что если молекулы находятся друг от
друга на расстоянии, на котором
межмолекулярные силы взаимодействия
не действуют (г),
то П=0. При постепенном сближении молекул
между ними появляются силы притяжения
(F0).
Тогда, согласно (60.1), потенциальная
энергия взаимодействия уменьшается,
достигая минимума при r=r.
При rrс
уменьшением rсилы
отталкивания (F>0)
резко
возрастают и совершаемая против них
работа отрицательна (A=FdrПотенциальная
энергия начинает тоже резко возрастать
и становится положительной. Из данной
потенциальной кривой следует, что
система из двух взаимодействующих
молекул в состоянии устойчивого
равновесия (r=r)
обладает минимальной потенциальной
энергией.
Критерием
различных агрегатных состояний
вещества является соотношение величин
Пmin
и kT.
Пmin
— наименьшая потенциальная энергия
взаимодействия молекул — определяет
работу, которую нужно совершить против
сил притяжения для того, чтобы
разъединить молекулы, находящиеся
в равновесии (r=r);
kTопределяет
удвоенную среднюю энергию, приходящуюся
на одну степень свободы хаотического
теплового движения молекул.
Если
Пmin0,
т.
е. вероятность образования агрегатов
из молекул достаточно мала. Если
IImin>>kT,
то вещество находится в твердом состоянии,
так как молекулы, притягиваясь друг к
другу, не могут удалиться на значительные
расстояния и колеблются около
положений равновесия, определяемого
r0.
Если ПminkT,
то
вещество находится в жидком состоянии,
так как в результате теплового движения
молекулы перемещаются в пространстве,
обмениваясь местами, но не расходясь
на расстояние, превышающее r.
Таким
образом, любое вещество в зависимости
от температуры может находиться в
газообразном, жидком или твердом
агрегатном состоянии, причем температура
перехода из одного агрегатного состояния
в другое зависит от значения Пmin
для данного вещества. Например, у инертных
газов Пmin
мало, а у металлов — велико, поэтому
при обычных (комнатных) температурах
они находятся соответственно в
газообразном и твердом состояниях.
Основные формулы термодинамики и молекулярной физики, которые Вам пригодятся
Основные формулы термодинамики и молекулярной физики, которые Вам пригодятся.
Вот он, еще один отличный день для практических занятий по физике. Сегодня, дорогие друзья, мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.
Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.
Идеальный газ
Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.
Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.
Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева
Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).
Универсальная газовая потоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)
Массу, в свою очередь, можно вычислить, как произведение плотности и объема.
Основное уравнение молекулярно-кинетической теории (МКТ)
Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:
Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:
Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ
Первое начало термодинамики. Формулы для изопроцессов
Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:
Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них
Изотермический – протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:
Изохорный – протекает при поcтоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.
Изобарный – идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:
Теплоемкость
Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.
Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.
Тепловые машины. Формула КПД в термодинамике
Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.
Коэффициент полезного действия тепловой машины вычисляется по формуле
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Шкала — абсолютная температура
Шкала абсолютных температур ( К) имеет только положительные отсчеты от абсолютного нуля — той температуры, ниже которой невозможно дальнейшее охлаждение физического тела. Измерение температур по этой шкале не зависит от физических свойств веществ, Применяемых для термометров.
Шкала абсолютных температур ( К) имеет только положительные отсчеты от абсолютного нуля — той температуры, ниже которой невозможно дальнейшее охлаждение физического тела. Измерение температур по этой шкале не зависит от физических свойств веществ, применяемых для термометров.
Шкалу абсолютных температур, у которой нижняя граница тем-ратурного промежутка определяется состоянием абсолютного коя молекул, называют термодинамической шкалой Кельвина.
В шкале абсолютных температур, имеющей широкое применение в термодинамике, расстояние между постоянными точками, как и в стоградусной шкале, разделено на 100 частей, нуль же шкалы перенесен на 273 деления ниже точки плавления льда.
Кельвина или по шкале абсолютных температур.
Если температуру выразить в шкале абсолютных температур ( градусы Кельвина), то логарифмическая зависимость получается почти прямолинейной.
Температуру Т отсчитывают по шкале абсолютных температур ( шкала Кельвина) от такого значения, принятого за нуль, по мере приближения к которому энергия хаотического теплового движения молекул также стремится к нулю. При этом сильно проявляются различные квантовые эффекты. При температуре, приближающейся к абсолютному нулю, наблюдается быстрое спадение теплоемкости, у ряда металлов-проявляется сверхпроводимость, жидкий гелий делается сверхтекучим.
Наряду со стоградусной шкалой применяется также шкала абсолютных температур, нуль которой лежит на 273 15 ( округленно 273) ниже температуры точки плавления льда. Температура, измеряемая по этой шкале, называется абсолютной, или температурой в градусах Кельвина. В обеих шкалах единица измерения ( градус) остается одной и той же.
Наряду со стоградусной шкалой применяется также шкала абсолютных температур, ноль которой лежит на 273 ( округлено) ниже температуры точки плавления льда. Температура, измеряемая по этой шкале, называется абсолютной, или температурой в градусах Кельвина. В обеих шкалах единица измерения ( градус) остается одной и той же.
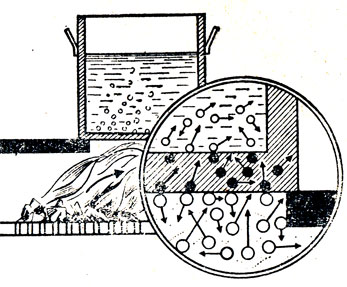
|
Схема открытой системы. |
Какое выражение является исходным для построения шкалы абсолютной температуры.
От абсолютною нуля начинается отсчет по шкале абсолютных температур, часто применяемой при научных и технических исследованиях. Градус ( СК) ее имеет такую же величину, как и градус обычной стоградусной шкалы ( СС), Нуль последней будет, следовательно, равняться 273 по абсолютной шкале.
От абсолютного пуля начинается отсчет по шкале абсолютных температур, часто применяемой при научных и технических исследованиях. Абсолютная шкала очень удобна, так как не содержит отрицательных температур.
От абсолютного нуля начинается отсчет по шкале абсолютных температур, часто применяемой при научных и технических исследованиях. Абсолютная шкала очень удобна, так как не содержит отрицательных температур.
Земные условия относятся к чрезвычайно холодному участку шкалы абсолютных температур, и химические превращения, в совокупности составляющие метаболизм, просто не могли бы происходить с достаточной для поддержания жизни скоростью, если бы не было биологических катализаторов, природу которых мы сейчас кратко рассмотрим.
1. Распределение энергии по степеням свободы
Выражение
для средней энергии молекулы газа
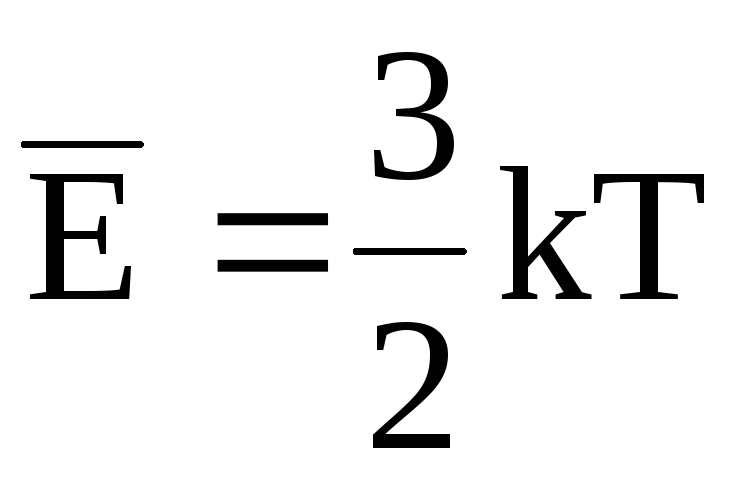 учитывает только её среднюю энергию
учитывает только её среднюю энергию
поступательного движения. Но наряду с
поступательным движением, молекула
может вращаться и совершать колебания.
Эти виды движения так же связаны с
некоторым запасом энергии, определить
который, можно пользуясь понятием
статистической физики о равном
распределении энергии по степеням
свободы.
Число
независимых координат, необходимых для
полного описания положения системы в
пространстве, называется
числом степеней свободы
(i).
Так,
например, движение точки, совершающей
перемещение по всей области пространства
в любой момент времени будет полностью
описано тремя координатами, т. е. она
обладает тремя степенями свободы (i=3).
Если на характер
изучаемого движения накладывать
некоторые ограничения, то число степеней
свободы уменьшается.
Так
для описания движения точки по поверхности
необходимо задать две независимые
координаты, т.е. движущаяся по поверхности
точка имеет две степени свободы (i
= 2).
Точка,
совершающая движение по прямой, имеет
одну степень свободы (i
= 1). В общем
случае точка или система точек наряду
с поступательным движением может
одновременно участвовать во вращательном
и колебательном движениях. Общее число
степеней свободы в этом случае будет
равно
 (12.1)
(12.1)
где
iп
— число степеней свободы поступательного
движения точки;
iвр
— число степеней свободы вращательного
движения точки;
iк
— число степеней свободы колебательного
движения точки ( );
);
iкп
— число степеней свободы колебаний точки
при поступательном движении;
iквр
— число степеней свободы колебаний точки
при вращательном движении.
По аналогии с механическими системами,
каждой молекуле, каждому атому газа
можно приписать определённое число
степеней свободы, рассматривая при этом
их как материальные точки. Так, одноатомная
молекула газа имеет только три степени
свободы поступательного движения (i= 3); двухатомная при упругой связи –
шесть степеней свободы (i= 6), а при жёсткой связи — пять степеней
свободы (i= 5);
трёхатомная молекула при жёсткой связи
между атомами имеет шесть степеней
свободы (i= 6).
Известно,
что средняя кинетическая энергия
поступательного движения молекул равна

Поступательное
движение описывается тремя степенями
свободы, а т.к. все степени свободы
равноправны, то на каждую из них приходится

(12.2)
Но
ни один из видов движения (поступательное,
вращательное, колебательное) не имеет
преимуществ перед другими. Следовательно,
можно утверждать: «На любую степень
свободы приходится в среднем одинаковая
энергия, а молекула, обладающая i степенями
свободы, будет обладать энергией
 ».
».
Данное утверждение называюттеоремой
о равномерном распределении энергии
по степеням свободы
(теорема Больцмана).